It’s not uncommon for students to come across problems that require finding the square root of a number. While it’s easy to rely on a scientific calculator or a smartphone, learning how to find square root by hand can help understand the concept of square roots at a deeper level. 

There are a few different ways of finding squares by hand, all of which were created before calculators came around.

We discuss three methods of finding square roots by hand in this post.

How to Find the Square Root of a Number?

The guess and check and prime factorization methods are both quick and easy methods to find the squared root of any number. The long division method is particularly helpful in finding the square roots of irrational numbers. 

Method #1: Guess and Check 

Finding the decimal approximation of a square root with guess and check involves:

1. Making an initial guess about the root value
2. Squaring the guessed root value
3. Determining how close the guess was to the number
4. Improving your guess by increasing or decreasing the guessed squared root accordingly

Since applying this method involves using the definition of a square root, it helps you understand the concept at a deeper level.

Let’s say you want to find √20. Since the √16 = 4 and √25 = 5, √20 lies between 4 and 5. Applying the guess and check method:

1. Let’s suppose √20 = 4.5.
2. 4.52 = 20.25. Therefore, √20 < 4.5.
3. Let’s assume √20 = 4.4.
4. 4.42 = 19.36. Therefore, √20 > 4.4.
5. Let’s assume √20 = 4.45.
6. 4.452 = 19.8025. Therefore, √20 > 4.45.
7. Let’s assume √20 = 4.47.
8. 4.472 = 19.9809. Therefore, √20 > 4.47.
9. Let’s assume √20 = 4.475.
10. 4.4752 = 20.02. Therefore, √20 < 4.475.

Continuing this process, we will find that √20 = 4.472135955.

Method #2: Prime Factorization

The prime factorization method involves finding what numbers make another number. The numbers that multiply together to make another number are called its factors.

To find the square root of any number with this method, you must find the number’s prime factors and then see if it has any perfect squared numbers (16, 49, 121, etc.)

Let’s assume you want to find √400. You must first find the prime factors of 400. You can do this with ease by continually dividing the number with prime numbers. 

We’ve illustrated the process with a factor tree:

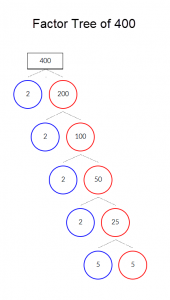
Image: Factor-Tree-of-400.png

The prime factors are 2, 2, 2, 2, 5, and 5. We must now determine whether 400 is a multiple of perfect squares. 

400 = 24 * 52 = 16 * 25

Therefore,

√400 = √16*25 = √16 *√ 25 = 4 * 5 = 20

While this looks easy, the method gets a little more complex when you find the square root of numbers that are not rounded, like 400.

If you try to find the square root of 147, the prime factors will be:

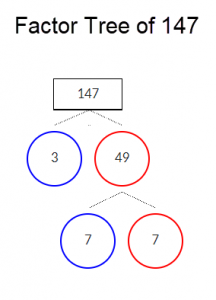
Image: Factor-Tree-of-147.png

The prime factors are 3, 7, and 7. We must now determine whether 400 is a multiple of perfect squares. 

147 = 72 * 3 = 49 * 3

Therefore,

√147 = √49*3 = √49 * √3 = 7*√3 = 7√3

Now, you will need to take the extra time to use the guess and check method and find the value of √3. We know that 12=1 and 22=4. So, √3 must be between 1 and 2.

1. Let’s suppose √3 = 1.5.
2. 1.52 = 2.25. Therefore, √3 > 1.5.
3. Let’s assume √3 = 1.7.
4. 1.72 = 2.89. Therefore, √3 > 1.7.
5. Let’s assume √3 = 1.73.
6. 1.732 = 2.9929. Therefore, √3 > 1.73.

Continuing this process, we get √3=1.732. 

7√3=7* √3 = 7*1.732 = 12.124

Therefore,

√400 = 7√3 = 12.124

You can also find the square roots of decimal numbers by simply writing the number as a fraction and finding the numerator and denominator’s prime factors.

Let’s say you want to find √17.64. You must first write it as √1764/100, and then find the prime factors of 1764 and 100. You can then divide the numbers and work out the answer, 4.2.

Method #3: Long Division

The long division method can seem difficult, but it makes calculating the rational approximations of irrational numbers uncomplicated. 

Here’s a quick illustration of using long division to find √3.

1. First, find the largest number whose square is less than or equal to 3. Then, use it as a divisor and write the remainder.
2. Place a point after the first digit in the quotient to indicate decimals.
3. Bring down two zeros to the remainder.
4. Now, guess the largest possible digit such that when the new divisor is multiplied with it, the product is less than or equal to the dividend.
5. Carry out the division to work out the remainder. 
6. Repeat the process from step 3 to calculate √3 to the decimal places you want.

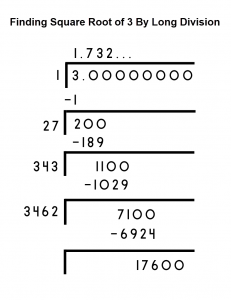
Image: Finding-Square-Root-of-3-By-Long-Division.png

Conclusion: The Fastest Method to Find Square Roots

All methods listed in this post are equally reliable, and you can use whichever method you find easiest to approach.

If you need to find the square root of a number quickly, you can use a calculator since calculators square root numbers in a matter of milliseconds. 

The Meta-Calculator Root Calculator works on any browser and can calculate the square root of any number in one click. 

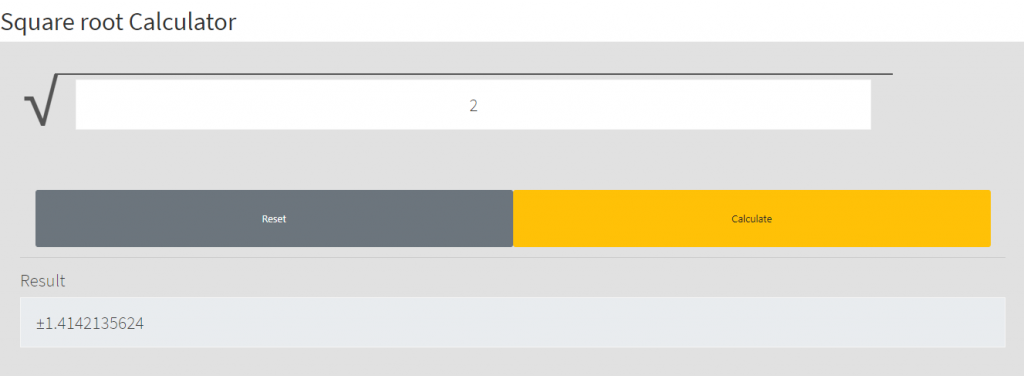
Image: Meta-Calculator-Root-Calculator.png

All you have to do is enter the number in the field and hit “Calculate.”