We encounter mathematics on a daily basis, and it has greatly influenced how we perceive the world. Equations are present everywhere and are essential to daily life, from Newton’s Law of Gravitation to the Black-Scholes model used by bankers to forecast the markets. A book titled “17 Equations That Changed the World” was published in 2013 by renowned author Ian Stewart. This book thoroughly discusses each equation that has impacted the path of human history.

A glimpse of these amazing equations that have influenced both mathematics and human history is provided below:
- The Pythagorean Theorem
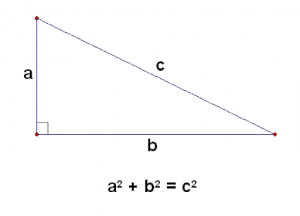
Photo Source: https://mathblog.com/reference
One of the first theorems that ancient civilizations were aware of was the Pythagorean Theorem. This well-known theorem is named after the Greek mathematician and philosopher Pythagoras, who made significant contributions to the fields of mathematics, astronomy, and music theory. (Texasflange.com)
This theorem is fundamental to how we comprehend geometry. When you square the lengths of the short sides, a and b, and put them together, you obtain the square of the length of the long side, c, which illustrates how the sides of a right triangle relate to one another on a flat plane. In some aspects, this connection truly distinguishes between curved, non-Euclidean geometry and our typical, flat Euclidean geometry. A right triangle drawn on the surface of a sphere, for instance, does not necessarily have to adhere to the Pythagorean theorem.
- Logarithms

Photo Source: https://virtualnerd.com/algebra-2
The logarithm is the power that a number must be raised to produce another number. For instance, the base ten logarithm of 100 is 2, since ten multiplied by two equals 100. Logarithms can be utilized to address issues that cannot be resolved using the notion of exponents alone since they are nothing more than another way to represent exponents.
The name “logarithm” was coined by Scottish mathematic John Napier (1550–1617) from the Greek words logos and arithmos, which combined to create the phrase “ratio-number.”
- Calculus
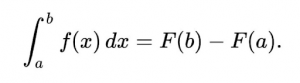
Photo Source: https://www.cbc.ca/radio
Mathematical models frequently employ calculus to find the best answers, which aids in understanding how a function’s associated values vary over time. Calculus is primarily built on the two ideas of derivatives and integrals. Calculus focuses on a number of crucial mathematical concepts like differentiation, integration, limits, functions, and so on. Newton and Leibniz created calculus, a branch of mathematics that examines the study of the rate of change.
- Law of Gravity

Photo Source: https://www.teepublic.com/poster
According to Newton’s Law of Universal Gravitation, every particle in the universe is drawn to every other particle with a force that is inversely proportional to the square of the distance between them and directly proportional to the product of their masses. The idea that gravity is a force that affects everything in the universe was initially put forth by Isaac Newton. That is why the law of universal gravitation—also known as Newton’s law of gravity—is therefore called. Because of universal gravity, the moon continues to orbit the Earth with the same force that causes an apple to fall from a tree to the ground. Additionally, because of the concept of universal gravitation, you may pull on the Earth as it pulls on you.
- Wave Equation
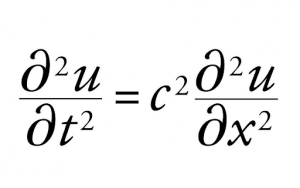
Photo Source: https://medium.com/intuition/the-intuition-behind-the-wave-equation-2550b58f55cf
One of the most crucial equations in mechanics is the wave equation. It depicts the movement of fluid surfaces, such as water waves, in addition to the movement of strings and wires. As waves exist in classical physics, such as mechanical waves (such as water, sound, and seismic waves) or light waves, the wave equation is a crucial second-order linear partial differential equation. It occurs in disciplines including fluid dynamics, electromagnetics, and acoustics.
- The square root of -1
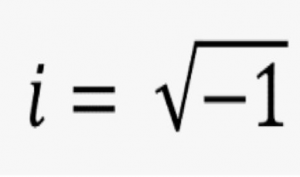
Photo Source: https://aminoapps.com/c/maths-amino
Mathematicians have long sought to broaden our understanding of what numbers truly are, moving beyond natural numbers to include fractions, negative numbers, and real numbers. (1) is represented by the imaginary letter i in mathematics. Since negative square roots don’t truly exist, we substitute the square root of -1 with the shortcut i, sometimes known as the “imaginary” number, since it is much simpler to keep writing than to type out the square root each time. In this approach, we save the “imaginary” number in case we need to square it, multiply it by another imaginary number, or do something else to make the number usable in a later equation.
- Euler’s Formula for Polyhedra
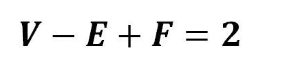
Photo Source: https://www.pinterest.ph/pin
V – E + F = 2, where V is the number of vertices, E is the number of edges, and F is the number of faces, is Euler’s formula for Polyhedra. The three-dimensional equivalents of polygons like the cube on the right are called Polyhedra. A polyhedron’s vertices are its corners, edges are the lines connecting the vertices, and faces are the polygons that cover it.
8 vertices, 12 edges, and 6 faces make up a cube. Edges are subtracted from faces and added back to vertices, giving me 8 + 6 – 12 = 2. If all of a (convex) polyhedron’s faces are identical to those of a regular polygon and all of its vertices are similarly surrounding, the polyhedron is said to be a regular convex polyhedron. The tetrahedron, cube, octahedron, icosahedron, and dodecahedron may all be made simply by experimenting with sticks.
- Normal Distribution
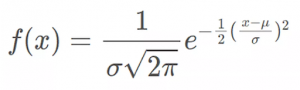
Photo Source: https://www.investopedia.com/terms
The most significant probability distribution in statistics for independent, random variables is the normal distribution, sometimes referred to as the Gaussian distribution. In statistical reports, its well-known bell-shaped curve is often recognized. A continuous probability distribution that is symmetrical around its meaning is known as the normal distribution. Most of the observations are concentrated around the center peak, and the probability of values that deviate from the mean in either direction tapers down evenly.
- Fourier Transform
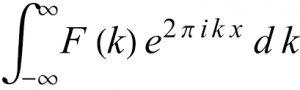
Photo Source: https://mathworld.wolfram.com/FourierTransform
A mathematical function known as the Fourier transform uses a time-based pattern as input to calculate the strength, rotation speed, and total cycle offset for each potential cycle. The Fourier transform is used to create waveforms, which are inherently functions of time, space, or another quantity.
To determine the fundamental frequencies that make up a wave, one can utilize the Fourier transform mathematical function. Think about playing a piano chord. When a chord is played, the sounds of the notes blend to create a sound wave. The waves of the various notes interfere with one another by adding or canceling at various places along the wave, which is how this works. A Fourier transform may identify the notes that make up a chord by taking this complex wave and determining the frequencies that created it.
- Navier-Stokes Equation
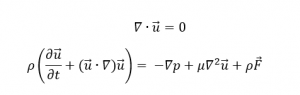
Photo Source: https://medium.com/navier-stokes-equations
The Navier-Stokes equation, a partial differential equation used to model the flow of incompressible fluids in fluid mechanics, characterizes this flow. Engineer Claude-Louis Navier of France added the concept of viscosity (friction) to the more complex and actual problem of viscous fluids in 1821. When Newton’s second law is applied to fluid dynamics, the equations result from the assumption that the stress, or internal forces, is the result of the addition of a diffusing viscous factor (depending on which direction the velocity is changing) and a pressure term.
- Maxwell’s Equation
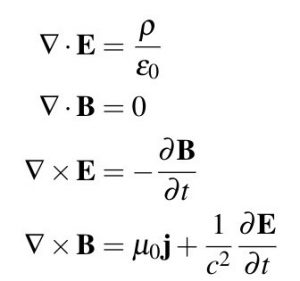
Photo Source: https://www.cantorsparadise.com/maxwells-equations
The four equations that makeup Maxwell’s equations explain how magnetic and electric fields behave and interact. James Clerk Maxwell published equations in the 1860s that show how charged particles produce an equal number of electric and magnetic forces. A field is a force per unit charge. The particles could be moving or still. These provide all the information necessary to compute the motion of classical particles in electric and magnetic fields, together with the Lorentz force equation.
- Second Law of Thermodynamics
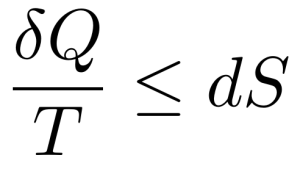
Photo Source: https://medium.com/illumination/the-second-law-of-thermodynamics-56a84456dcf9
According to the second rule of thermodynamics, entropy (disorder) increases as matter flows freely or energy changes forms. After a period, variations in temperature, pressure, and density tend to balance out horizontally. Gravity prevents pressure and density from being evenly distributed vertically. On the bottom, there will be more pressure and density than on the top. Entropy is a measurement of how evenly matter and energy are dispersed over all available space.
- Relativity
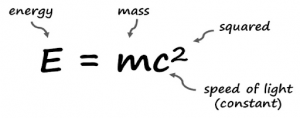
Photo Source: https://energywavetheory.com/equations/emc2/
Albert Einstein released the General Theory of Relativity, sometimes known simply as “general relativity,” 10 years after the special theory of relativity was developed. The concept of spacetime is used in Einstein’s general theory of relativity. Having a four-dimensional cosmos with three spatial (space) dimensions and one temporal (time) dimension is referred to as spacetime. Every physical event has a specific location within these three spatial dimensions, as well as a certain temporal component. The general theory of relativity states that any mass bends spacetime, and that any other mass moves in the same direction as these curves. More curvature results from the larger mass. This provided a fresh explanation of gravity.
- Schrodinger’s Equation
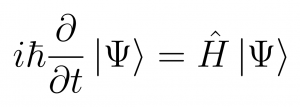
Photo Source: https://medium.com/quantafy
The Schrodinger equation is a mathematical formula that Erwin Schrödinger developed in 1925. It serves the same purpose as Newton’s laws and the conservation of energy in classical mechanics by foretelling how a dynamic system will behave in the future. In terms of the wavefunction, it is a wave equation that accurately and analytically forecasts the likelihood of occurrences or outcomes. The precise conclusion is not predetermined, but the Schrodinger equation may forecast the distribution of outcomes given in many occurrences.
- Information Theory
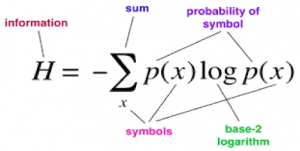
Photo Source: https://www.cantorsparadise.com/intro-to-information-theory
The mathematical treatment of the ideas, parameters, and regulations regulating the transmission of messages through communication networks is known as Information Theory. Claude Shannon established it in the middle of the 20th century, and since then it has developed into a robust area of mathematics that has assisted the growth of several other scientific disciplines, including statistics, biology, behavioral science, neurology, and statistical mechanics. Some people consider information theory to be a subset of probability theory since the methods utilized in it are probabilistic in nature. The data in a message describing one of a set of potential occurrences quantifies the symbols required to represent the event in the best feasible way.
- Chaos Theory
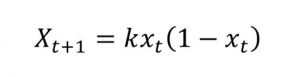
Photo Source: https://www.sciencealert.com/the-17-equations-that-changed-the-course-of-history
Mathematics includes the field of chaos theory. It examines several extremely delicate systems. A relatively minor adjustment could cause the system to act quite differently. After some time, even very slight modifications to the initial state of a chaotic system have a significant impact. Due to the fact that weather changes and errors might occur, even the most sophisticated computers can only predict the weather a few days in advance. The “butterfly effect” is commonly used to describe chaotic systems since even a single butterfly may produce enough wind to alter the weather. No computer has sufficient knowledge to predict how a slight breeze will affect the weather.
- Black-Scholes Equation
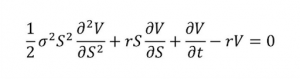
Photo Source: https://www.quora.com/What-is-the-significance
The Black-Scholes Equation is frequently used to price option contracts and is sometimes known as the Black-Scholes-Merton (BSM) model. The current stock price, the period till expiry, the risk-free rate, and volatility are the five input variables used by the Black-Scholes model. It was created in 1973 and is currently recognized as one of the finest techniques for determining the price of an option contract.